Mindful learning
No hands up please
21/09/11 02:18

Chatting after the lesson, the teacher was bemused over Tony’s willingness, as he wasn’t that mathematically confident.
Having watched the lesson unfold it was clear that the teacher did what many teachers do: wait for several children to put their hands up before selecting someone to answer. I think Tony had figured out that the easiest way NOT to get picked was to be the first person to volunteer the answer.
The routine of ‘hands up’ is so ubiquitous in maths lessons that it can seem as natural as the sky looking blue, water feeling wet and Cliff Richard staying young.
But just because ‘it’s always been that way’ isn’t a good reason to carry on with some classroom practices. And there is good evidence that ‘hands up’ may not be the best practice.
How do you know if you are good at maths?
Dropping into a maths class I will often ask the children this question. There is a remarkable degree of agreement in the answers, which are usually along the lines of:
You’re good at maths if you can do it quickly and easily.
The practice of ‘hands-up’ for answers perpetuates the belief of speed as being the essence of being good at maths. Children who need a bit longer to figure things out simply don’t have the time they need or are discouraged when others around them get a hand up first.
The psychologist Carole Dweck has looked at the downside of such an attitude to learning and one of her perhaps surprising findings is that such beliefs hamper successful students as much as the less successful.
If you’ve been successful at school maths because you can do what is set without much effort, then what happens when the time comes (and it will) that you meet some maths that isn’t easily done and requires more effort? Dweck’s research shows that many learners then think along the lines of ‘perhaps I was wrong, I ‘m not that good at maths after all’ and conclude that maybe maths isn’t for them.
Behind this, Dweck argues, is whether learners view mathematical ability as a gift—something that you either have or not - or whether they view it as something that can be developed through practice and effort - a growth mindset.
The message is clear over-emphasis on quick answers perpetuates the ‘gift’ view of mathematical ability. ‘ Hands up’ leads to everyone losing out mathematically: the lower attainers in the short term, the higher attainers long-term.
A quiet ’thumbs up’ (held still against the chest) can still signal to the teacher when learners are ready, provide a calmer space within which to think, and dispel the myth that mathematical ability is all about speed.
blog comments powered by Disqus
Comments
Mindful mathematics
04/06/11 10:05
Ellen Langer
I was lucky this week to hear the wondrous Ellen Langer give a talk. If you haven’t come across it, then I highly recommend her book ‘The Power of Mindful learning’. She spoke for over two hours and it was pure enchantment.
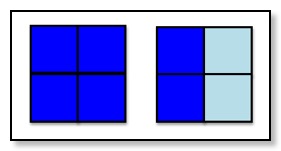
One of the key findings from Prof Langer’s research of over 30 years is that learning is more powerful if we are mindful of the conditionality of most ‘facts’. For example, in a lesson on fractions, a diagram like the one above is usually introduced as the pale blue shows ½. In contrast, Langer argues that presenting the diagram as it ‘could’ represent ½ makes the learning mindful and deeper.
Part of the argument for this is that the ‘fractions’ are not in the diagram itself but they are the result of someone somewhere at sometime deciding how the diagram should be read. In other words, there was a choice to be made over what mathematics the diagram could represent - not what it does represent.
By re-introducing this choice and conditionality into the teaching of it, the learner is encouraged not simply to take the mathematics for granted, nor to just commit something to memory. In contrast they engage in mathematical thinking.
So what else could the pale blue represent?
Well, it could be different if we are mindful of not taking for granted the condition that the ‘unit’ has to be four small squares. Under the condition of the whole picture as the unit, then the pale blue could be ¼.
Or we could set up the condition of comparing the pale blue to the dark blue and so the pale blue could be ⅓. The possibilities do not end there.
Of course this does not mean telling children that ‘anything goes’ and they are free to choose any reading they like. But by implicitly acknowledging in our teaching the human agency in mathematics we could help more learners come to see mathematics as a human endeavour worth engaging with, rather than something to keep at arm’s length.
blog comments powered by Disqus